Цена отклонений при размещении ставок

Как узнать ценность ставки после ее размещения? Понимание цены отклонений поможет вам повысить доход от игры на ставках в долгосрочной перспективе. Для того чтобы узнать больше, прочитайте эту статью.

В попытках найти ответ на поставленные выше вопросы не так давно я сформулировал определение полезной величины для серьезных игроков на ставках, назвав ее «эквивалентом свопа». Нашей целью станет расчет корреляции между ожидаемым значением (EV) рискованных ставок и соответствующим эквивалентом надежности (CE). Умножьте ожидаемое значение ставки на эквивалент свопа – и вы получите эквивалент надежности (т. е. объем принадлежащих вам денежных средств, возможностью обладания которыми вы можете пренебречь в пользу размещения ставки). Кроме того, вы можете не только выполнить это весьма важное преобразование, но и применить полученную величину для расчета цены отклонений.

Большинству людей сама идея отклонений кажется непонятной и загадочной, но для интеллектуальных игроков на спортивных ставках это понятие воплощает в себе неизбежные увеличения и уменьшения прибыли на пути к заветному капиталу, ждущего игрока в конце пути. Все дело в том, что отклонения – это не просто раздражающая особенность, с наличием которой следует смириться для формирования теоретического представления о доходности по вложениям (ROI). На самом деле у этих отклонений есть своя цена. Откуда же она берется? Если бы цены отклонения не существовало, то эквивалент надежности для любой существующей ставки в любой выбранный момент времени соответствовал бы ожидаемому значению. Как я уже упоминал в нескольких своих предыдущих статьях, эти показатели не тождественны друг другу.

Мы можем определить действительную цену отклонения (CoV) как разность между значениями EV и CE, и хотя числовое выражение этой разности в случае с отдельными ставками обычно представляет собой крошечный процент банкролла, на протяжении долгого срока даже этот процент может превратиться в существенную долю прибыли. Давайте используем уравнения для представления эквивалента свопа. Можно утверждать, что соблюдаются оба приведенных ниже равенства:

Мы можем объединить их и увидеть, что истинная цена отклонения равна значению EV, умноженному на (1 – эквивалент свопа):

Например, пускай букмекерская контора АБВ предлагает линию на сегодняшний бейсбольный матч между «Даймондбэкс» и «Рокиз» со следующими коэффициентами: «Даймондбэкс» +130 / «Рокиз» –150 (в десятичных коэффициентах – «Даймондбэкс» 2,30 / «Рокиз» 1,60). Вам известно, что согласно предоставленным Pinnacle сведениям, игроки «Рокиз» победят с 60%-й вероятностью. Теоретически вы можете разместить ставку на «Рокиз» в букмекерской конторе АБВ и добиться равного 0 итогового значения EV (т. е. ожидаемое значение для вашей ставки будет равно сумме вашей ставки). Вы могли бы подумать, что в результате многократного размещения одной и той же ставки с нейтральным значением EV убытки и доходы уравновесят друг друга, и подобный процесс ничем не будет отличаться от хранения денег в своем кармане.

Однако эти цифры не отражают полной картины. Они могут сообщить нам всего лишь об одном аспекте сферы размещения ставок: об измерении цены. Существует абсолютно другой аспект, который сильно влияет на решения игрока: риск. Если вы размещаете ставку какого угодно размера на «Рокиз», то при любом ожидаемом значении ставки ваши деньги попадают в зону риска, и возможность вернуть их обратно будет в некоторой мере зависеть от наличия отклонений. Так чем же нам приходится платить за эти отклонения? Давайте разберемся в этом вместе.

Предположим, что ваш банкролл составляет 1000 $, и так как значение EV говорит об отсутствии убытков, вы размещаете ставку на «Рокиз» размером в 50 $. Вы выигрываете в 60 % случаев (получая при этом 83,33 $) и проигрываете в 40 % случаев (не получая ничего). Ожидаемое значение банкролла после игры будет рассчитываться следующим образом:

Чему же будет равен эквивалент свопа для вашего купона после размещения ставки? Значение этого коэффициента мы также можем рассчитать:

Определим переменные:

w = выплата по ставке в виде процента от банкролла

p = вероятность выигрыша по ставке (в нашем примере соответствует 60 %)

Ваша выплата, w, будет равна 83,33 $ / 950 $ = 0,088, так как после размещения ставки оставшийся банкролл будет равен 950 $. Хотя значение EV для вашего купона равно 50 $, показатель CE составляет всего лишь (50 $ × 98,5 %) или же 49,25 $. Теперь мы можем выразить цену отклонений для вашей ставки:

«Скользкая дорожка» для вашего банкролла

Пусть эта величина и может показаться несущественной суммой, но если вы регулярно будете размещать аналогичные ставки, ваши убытки будут накапливаться, каждый раз увеличиваясь (теоретически), и рано или поздно вы окажетесь в проигрыше. Если выполнить моделирование этой ставки 10 000 раз, то в 81,6 % случаев ваш банкролл окажется растрачен (ниже приведен график для пяти типичных сценариев моделирования).

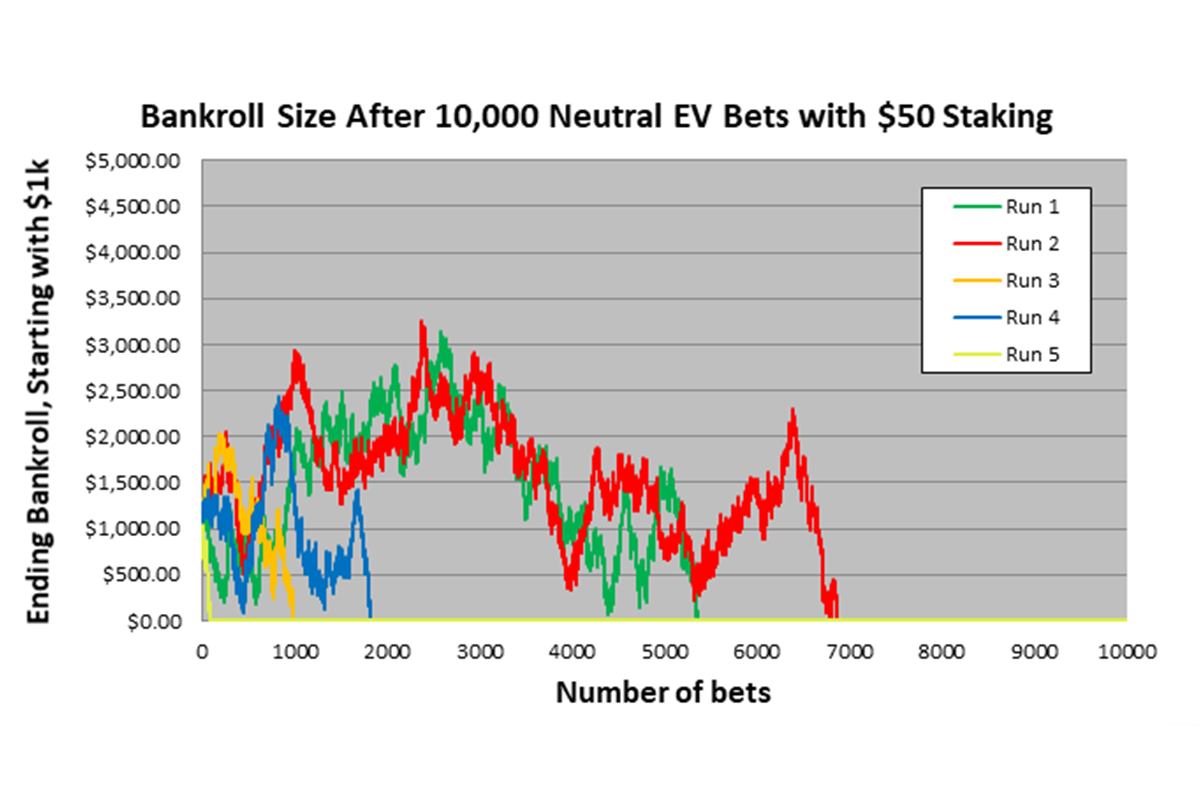
Для того чтобы получить более интуитивно понятное представление о процессах, попробуйте рассчитать, чему будет равен ваш банкролл при выигрыше и при проигрыше. Если вы выигрываете, ваш банкролл увеличивается до 1033 $, так что в следующий раз ставка размером в 50 $ будет представлять собой всего лишь 4,8 % банкролла. Если же вы проиграете, то банкролл уменьшается до 950 $, и следующая ставка величиной 50 $ равна 5,3 % банкролла. Выходит, что при размещении последующих ставок вы рискуете все меньшей долей своего банкролла в случае выигрышей и все большей долей в случае проигрышей – эта небольшая разница в конце концов превращается в постоянно увеличивающийся снежный шар, отнимающий огромные части вашего банкролла, если вам сопутствует череда неудач. Подобные закономерности отнюдь не помогают найти магическую формулу для обретения богатства или хотя бы для беспроигрышной игры.

Вы можете предположить, что проблему удастся устранить благодаря размещению пропорциональных ставок: стоит всего лишь постоянно выбирать в качестве суммы ставки 5 % текущего банкролла вместо фиксированных 50 $ – тогда при выигрышах получится размещать больше, а при проигрышах – меньше, и в итоге такие ставки будут уравнивать друг друга. Кроме того, если не размещать в виде ставки 100 % своего банкролла, то и разориться не получится, правильно? Эта теория, конечно же, выглядит неплохо. Но выдерживает ли она критику? Сперва давайте определимся с пониманием состояния «разорения». Разумеется, что при использовании пропорционального размещения ставок вы никогда не потратите свой банкролл полностью. Однако что вы почувствуете, когда ваш запас средств сократится до 10 $? Наверняка вам придется признать, что вы «разорились». Давайте выполним другое моделирование, в котором игрок будет регулярно размещать в виде ставки 5 % текущего банкролла с сохранением прежних условий, однако на этот раз окончательным проигрышем будет считаться момент, при котором банкролл опустится ниже 10 $. Как вы думаете, чем закончится такое моделирование?

Его результаты окажутся даже более печальными. Так как вы размещаете более крупные ставки после выигрышей, возможные суммы проигрышей тоже увеличиваются, даже если сперва вам и будет везти (пожалуй, везение – это единственная возможность не разориться спустя 10 000 ставок). Таким образом, чаще всего вы будете сталкиваться с результатом, подобным представленному на диаграмме ниже (для упрощения понимания ось Y представлена в логарифмическом виде), – в 88 % случаев игрок неизбежно разорится:

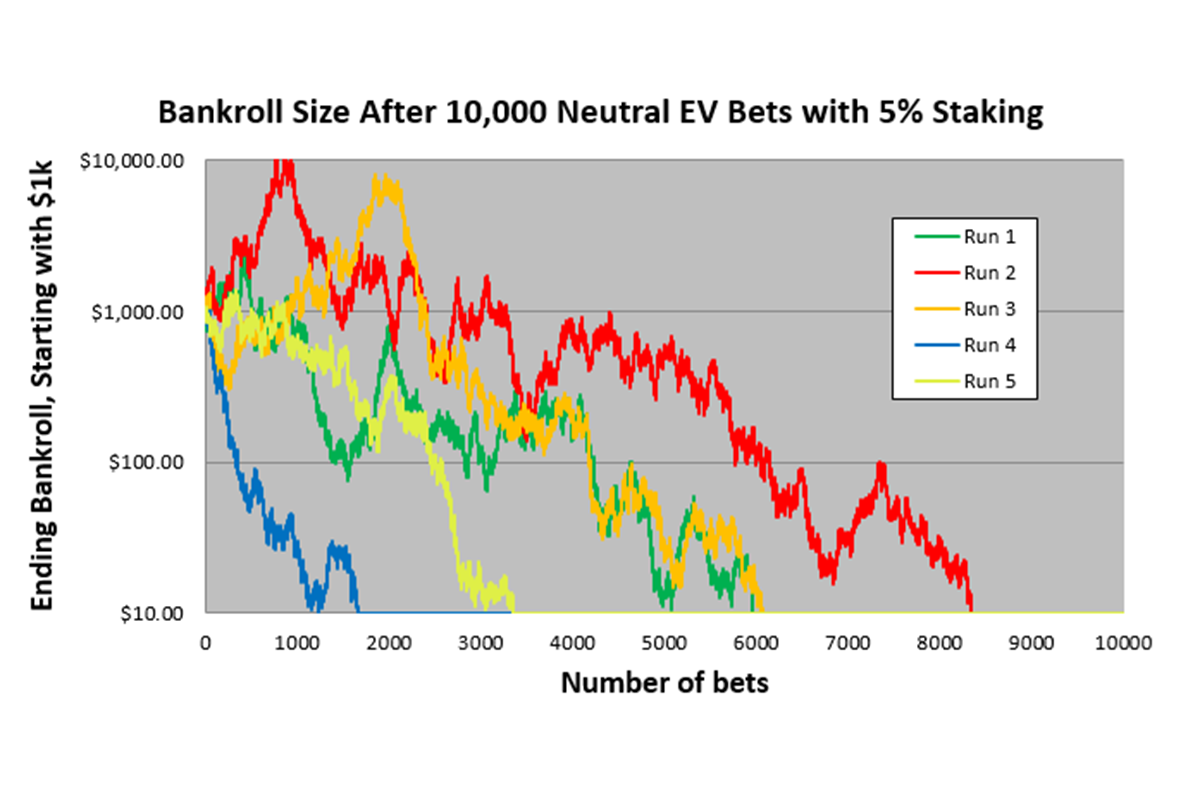
Вряд ли подобная тенденция вас удивит. Учитывая довольно крупное процентное значение ставки и отсутствие преимущества, ожидаемый прирост прибыли (EG) для однократного размещения ставки составляет –0,083 %. Пусть это число и не кажется большим, но после 5600 ставок ваш банкролл размером в 1000 $ в среднем уменьшится до 10 $. Если вы попытаетесь рассчитать ожидаемое значение ROI для тех же коэффициентов, но с преимуществом величиной 3,3 %, вы увидите, что дробный критерий Келли достигает целых 5 % для ставок на «Рокиз», и значение EG равно +0,083 %. Этот показатель равен значению –EG из моего примера (с учетом инверсии знака), так что размещение ставок с нейтральным значением EV расстроит вас настолько же сильно, насколько порадует размещение ставок с преимуществом величиной 3,3 %.

Я не пытаюсь сказать, что размещение ставок на линии с нейтральным значением EV – худшая ошибка, которую вы можете допустить, или что это решение выглядит таким же плохим, как и случайное размещение ставок на рынке, маржа которого превышает 4 %. Впрочем, если вы не обладаете бесконечным банкроллом, то вам не стоит полагаться на прибыльность своих ставок, ожидая того момента, когда они сравняются с математическим значением EV. Вам следует сосредоточиться на выборе такой суммы риска, которая теоретически может быть покрыта суммой выигрыша.

Если бы вы были не среднестатистическим игроком на ставках, а Джеффом Безосом, который может позволить себе банкролл в размере 100 миллиардов долларов, то эквивалент свопа для вашего ставочного купона мог бы равняться 100 %, ведь экономических последствий риска для ваших ставок не существовало бы. Ваш эквивалент свопа и цена отклонений выглядели бы так:

Заключение

Если понять, что у отклонений есть вполне реальная цена, станет проще осознать, почему вам не следует фокусироваться на поиске ставок с положительным EV и игнорировать ставки с нейтральным или отрицательным EV. Риск наличия отклонений, которые представляют собой нечто вроде комиссии или отчислений, сопутствующих торгам на бирже, может стоить вам денег, так что путем снижения риска вы всегда сможете получить дополнительную реальную выгоду. Иногда этот метод приводит к снижению суммы ставок, но даже если вы правильно будете выбирать размер ставки (предпочитая оптимальный размер или даже более малый), все равно вы будете попадать в такие ситуации, где EV ваших ставок изменяется и начинает существенно превышать эквивалент надежности.

В таких случаях хеджирование рисков (размещение ставок на другой вариант выбора у букмекеров с низкой маржой, таких как Pinnacle, или продажа части либо всей вашей ставки на бирже) может стать неплохой страховкой. Если же цена реализации подобной политики обладает меньшим значением, чем цена отклонений, то куда больше выгоды может принести покупка ставок.

Аналитические материалы предоставлены БК Pinnacle.