Как долго может продлиться серия поражений в ставках?

Все игроки должны иметь дело с потерями, независимо от того, насколько они квалифицированы. Некоторые из них могут встречаться с проигрышными сериями, которые длиннее, чем другие, но как долго может продлиться серия поражений в ставках? Читайте дальше, чтобы узнать.

Выиграть любое пари - это приятное чувство. Проигрыш, однако, считается вдвойне болезненным, с психологической точки зрения. Часто реакция игрока на проигрыш, особенно серию проигрышей, может привести к опрометчивому поведению, когда он либо ставит чаще, либо ставит больше денег, в попытке восстановить свои потери.

Даже для потенциально квалифицированных игроков с положительными ожиданиями ставок на их стороне, проигрышные раунды могут привести их к иррациональному сомнению эффективности своей стратегии. Гораздо легче усомниться в себе после 10 из 10 проигрышных ставок, чем после 10 из 10 выигрышных, хотя в статистических терминах они будут иметь очень схожие вероятности исхода. Вряд ли кто-то потрудится подвергнуть сомнению сверхэффективную систему.

Мы уже писали о просадках ставок и о том, как ими можно управлять. В этой статье мы хотим дополнить эту работу простым моделированием проигрышных серий, и, говоря более конкретно, как долго может одна из них продлиться.

Мы будем использовать последовательный прогон k проигрышных ставок в выборке из n ставок с одинаковыми коэффициентами, хотя нет никаких причин, по которым нельзя было бы расширить его, чтобы охватить более сложные периоды проигрыша и более сложные записи ставок с переменными коэффициентами с использованием моделирования Монте-Карло. Однако, по крайней мере, при простейшей проигрышной серии мы можем предложить некоторые основные математические формулы для ее описания, трудные при более сложных сценариях.

Вероятность проигрыша

Давайте рассмотрим игрока, который достаточно опытен, чтобы быть безубыточным в долгосрочной перспективе. Другими словами, он получает справедливые шансы. Таким образом, его шансы на выигрыш будут отражать "истинную" вероятность результата. На самом деле, то, что следует дальше, не очень меняется ни для неквалифицированных игроков, делающих ставки не глядя на маржу, ни для опытных игроков, которым удается найти предельное прибыльное ожидание. Причина в том, что подавляющее большинство того, что происходит в ставках, является следствием случайности. Коэффициент 2,0 означает вероятность 50%, коэффициент 4,0-25% и так далее. Вероятность выигрыша k последовательных ставок каждая с коэффициентом О задается следующим образом: 1/Оᵏ.

Например, вероятность выигрыша пяти подряд честных четных ставок с коэффициентом 2,0 равна 1/32.

Но здесь нас интересуют проигрышные ставки. При коэффициенте 2,0 вероятность проигрыша будет одинаковой, так как вероятность выигрыша или проигрыша составляет 50%. В более общем плане шансы на победу и поражение не одинаковы. Учитывая, что вероятность проигрыша равна 1 минус вероятность выигрыша, следует, что шансы проигрыша задаются выражением: О/О – 1.

Таким образом, вероятность проигрыша k последовательных ставок (каждая с коэффициентом О) задается следующим образом: (О – 1/О)ᵏ.

Ожидание проигрышных последовательностей

Какова вероятность наличия k (или более) последовательных проигрышей в выборке из n ставок с коэффициентом О? Оказывается, математика для этого вовсе не тривиальна. Но мы можем задать вопрос немного по-другому, и тогда математика намного проще. Вместо этого давайте спросим, сколько раз мы можем ожидать проигрыша k последовательных раз в выборке из n ставок с коэффициентом О?

Рассмотрим простой пример. Сколько раз мы можем ожидать проигрыша трех ставок подряд, каждая с коэффициентом 2,0, в серии из 10 ставок? Мы уже знаем, что вероятность единственного проигрыша трех подряд равна 1/8. Однако в серии из 10 ставок есть множество возможностей построить проигрышную последовательность из трех ставок. Это может произойти на ставках один, два и три, или на ставках два, три и четыре, и так далее вплоть до ставок восемь, девять и десять.

В этом примере было бы в общей сложности восемь возможных последовательностей, поэтому ожидаемое количество раз, когда мы будем иметь такую последовательность в 10 ставках, равно 8/8 или единице. Другими словами, в среднем мы ожидаем, что у нас будет одна проигрышная последовательность из трех ставок каждые десять ставок. Иногда их будет больше, а иногда и вовсе не будет, но в среднем будет одна.

В более общем виде число возможных последовательных позиций в серии из n ставок равно n – (k – 1) или n – k + 1.

Следовательно, ожидаемое число проигравших k последовательных ставок, назовем его e_k, в выборке из n ставок будет задано следующим образом:

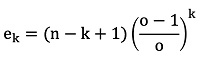
По мере увеличения числа ставок n для меньших значений k (при этом k всегда будет намного меньше n для проигрышных последовательностей, которые реально возможны и которые нас интересуют), e_k  будет стремиться к:

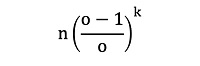
Например, для выборки из 1000 ставок с коэффициентом 2,0 ожидаемое число проигрышных последовательностей из пяти ставок будет равно 31,25 (31,125 по более точной формуле), округленное до 31 в качестве ближайшего целого числа.

Поскольку число ставок n примерно пропорционально ожидаемому числу проигрышных последовательностей длины k, мы ожидаем около 62 проигрышных серий из пяти ставок в 2000 ставках, и около 93 в 3000 ставках.

Когда e_k = 1, мы можем описать k как величину самой длинной проигрышной последовательности, которую обычно ожидают увидеть в выборке из n ставок. Для 1000 ставок с коэффициентом 2,0 ожидаемая самая длинная последовательность проигрышей будет log₂1000 = 9,97 или 10 до ближайшего целого числа. Другими словами, в выборке из 1000 ставок мы обычно можем ожидать, что самая длинная последовательность проигрышей будет состоять из 10 ставок.

При коэффициенте 3,0 ожидаемая самая длинная проигрышная последовательность будет равна 17, а при коэффициенте 5,0 - 31. Коэффициент 5,0 вполне типичен для игроков, делающих ставки на скачки. Как вы думаете, вы могли бы справиться с последовательностью из 31 неудач подряд, не струсив из-за того, что вы делаете?

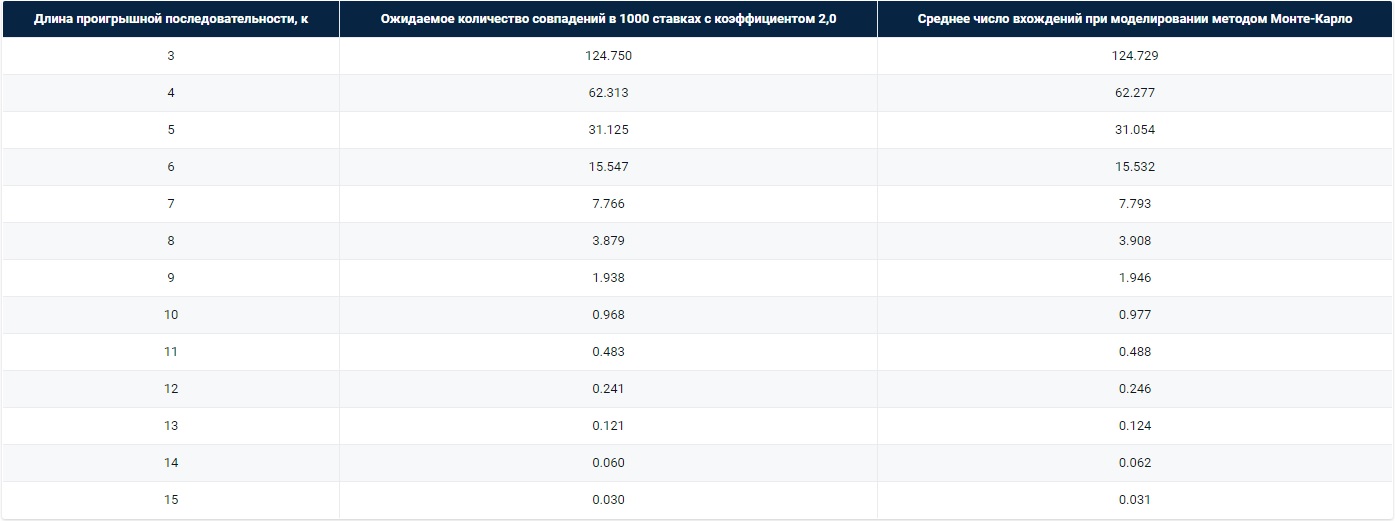
Мы провели 10 000 итераций моделирования Монте-Карло, чтобы проверить математику для e_k. В Таблице ниже сравниваются результаты для различных значений k. Существует почти точное совпадение между предсказанными случаями проигрышных последовательностей, основанными на математической формуле выше, и моделированием Монте-Карло:

На приведенном ниже Графике 1 мы построили зависимость между k и e_k для различных коэффициентов выигрыша. Ось y, e_k логарифмична. Прямая линия подтверждает, что k обратно пропорциональна логарифму e_k что в точности соответствует математическим ожиданиям. Точка, в которой каждая линия пересекает ось x (при e_k = 1), является ожидаемой самой длинной проигрышной последовательностью:

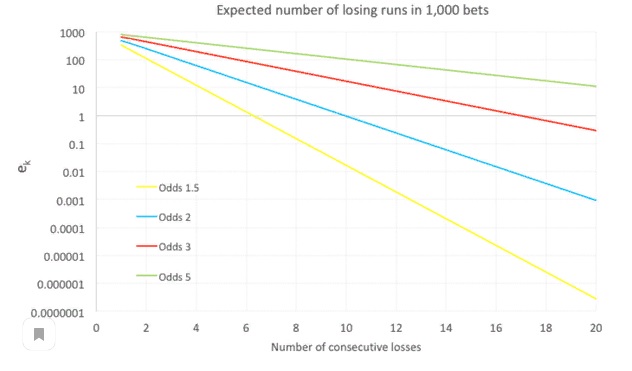
Учитывая приведенное выше приближение для k, ожидаемая самая длинная проигрышная последовательность в выборке из n ставок, таким образом, также пропорциональна логарифму n, как показано на следующем Графике 2. Таким образом, k удваивается с каждым квадратом n:

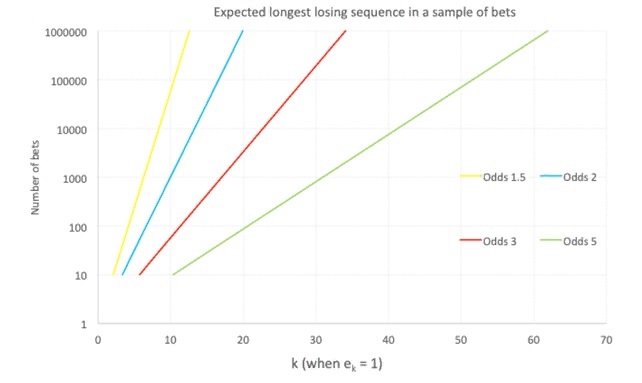
Вероятность проигрышной последовательности

Знание ожидаемого числа проигрышных последовательностей – это одно, но мы все еще не знаем вероятности их возникновения. Как уже упоминалось ранее, математика для этого нетривиальна, потому что частотное (вероятностное) распределение числа проигрышных последовательностей длины k в n ставках вовсе не очевидно, и будет отличаться для каждой длины k.

Например, мы можем знать, что в среднем увидим около одной проигрышной последовательности из 10 ставок в выборке из 1000 ставок на честные коэффициенты (без учета маржи), но это всего лишь среднее значение. Часто мы не увидим ни одной такой серии, иногда их может быть две, иногда пятб и более. Вместо этого гораздо проще прибегнуть к нашему надежному моделированию Монте-Карло.

С помощью 10 000 итераций моделирования Монте-Карло мы подсчитали, сколько раз каждая проигрышная полоса длиной k не наблюдалась. Например, для k = 10 в выборке из 1000 ставок максимальная проигрышная последовательность была короче в 6086 случаях, а 10 или более на остальных итерациях модели.

Полагаясь на закон больших чисел, это означает, что увидеть проигрышную последовательность из 10 или более ставок имеет шанс примерно 39%. Это кажется интуитивно правильным, если мы вспомним, что ожидание состоит в том, чтобы увидеть полосу проигрыша в 10 ставок примерно один раз в такой выборке. На Графике 3 ниже показано, как вероятность увидеть полосу проигрыша длиной k или более изменяется с k:

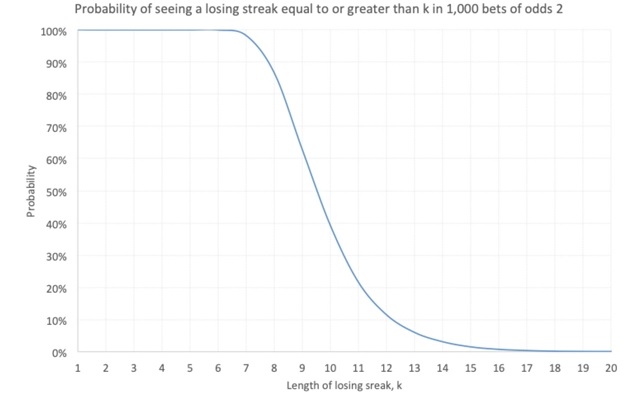
Очевидно, чем больше выборка ставок, тем больше вероятность того, что в какой-то момент произойдет что-то плохое. Мы знаем, что вероятность 10 последовательных проигрышей в 1000 ставках составляет 39%. Но каков бы был процент для меньших или больших выборок? Мы запустили еще одну симуляцию Монте-Карло, чтобы выяснить это. Приведенный ниже График 4 предназначен для k = 10:

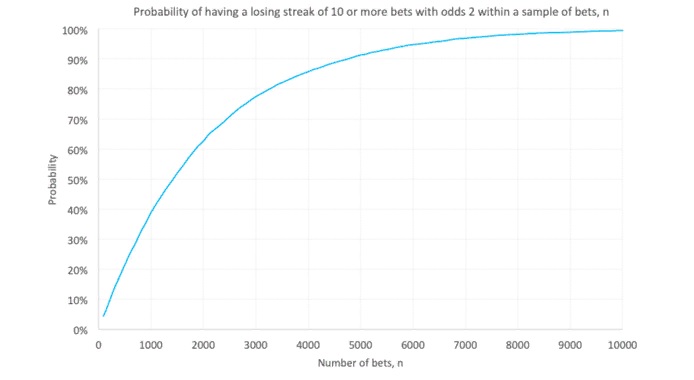
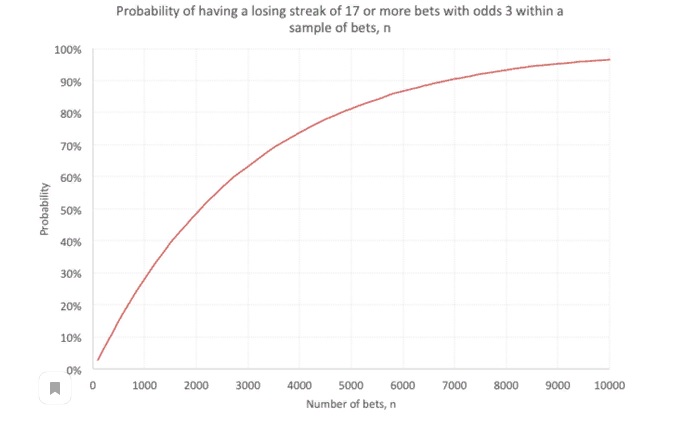
Мы можем повторно запустить нашу модель для любого значения k или любого набора коэффициентов. Другой пример выборки показан ниже на Графике 5для коэффициентов 3,0 и проигрышной полосы 17 или более:

Анализ проигрышных серий с реальными историями ставок в мире

До сих пор этот анализ был скорее теоретическим в том смысле, что он рассматривает только образцы ставок, где все коэффициенты одинаковы. Это может быть разумным предположением для игроков, предпочитающих ставки с точечным спредом и азиатским гандикапом, но менее вероятно для игроков на денежные линии с фиксированными коэффициентами. 

Конечно, мы могли бы использовать моделирование Монте-Карло, чтобы определить наши ожидаемые последовательности потерь, но есть ли способ использовать математику? Увы, мы не можем использовать средние коэффициенты для нашей выборки, потому что они будут непропорционально взвешены по отношению к более длинным коэффициентам.

Вместо этого мы должны использовать обратную среднюю из подразумеваемых вероятностей для всех коэффициентов. Например, если в нашей выборке есть пять ставок с коэффициентами 2,0, 3,0, 5,0, 10,0 и 20,0, вычислите подразумеваемые вероятности (0,5, 0,333, 0,2, 0,1 и 0,05), возьмите их среднее значение (0,237) и инвертируйте (О = 4,23).

Мы сделали это для выборки из 9 436 ставок. При вычисленном значении О = 2.66 с использованием приведенного выше метода наблюдалось отличное совпадение между ожидаемыми значениями для k и фактическими проигрышными последовательностями.

Математика предсказала 898 проигрышных последовательностей по меньшей мере из пяти ставок, но на самом деле их было 889. Аналогично, для k = 10 математика предсказала цифру 85; их и было ровно 85. При k = 9 прогноз составлял восемь, фактический - девять. Ожидаемая самая длинная проигрышная последовательность (e_k = 1) была предсказана равной 19. Самая длинная проигрышная последовательность была действительно 19, и состоялась только раз.

Что мы узнали о проигрышных сериях в ставках?

Надеемся, что этот довольно теоретический анализ последовательности ставок послужит напоминанием о том, что чем дольше вы ставите, тем больше вероятность того, что вы увидите более длинные полосы проигрышей.

Помимо поиска ожидаемой ценности, задача любого успешного игрока состоит в том, чтобы разумно управлять своими ожиданиями и научиться справляться с неизбежными неудачными сериями, которые способны существенно повлиять на его психологию. Знание того, чего ожидать и как это оценивать, по крайней мере, дает вам некоторую подготовку в этом отношении.

Аналитические материалы предоставлены БК Pinnacle.